How to : un réseau neuronal artificiel peut-il rivaliser avec Bach ?

Pendant que des chercheurs en intelligence artificielle organisaient leur Eurovision 2.0 pour faire s’affronter treize équipes issues de huit pays autour de l’AI Song Contest (concours musical similaire à l’Eurovision mais dans lequel chaque morceau a été élaboré à l’aide de systèmes d’intelligence artificielle), j’ai voulu générer des musiques reprenant le style de mes artistes préférés et ainsi créer de nouvelles œuvres musicales artificielles.

Je me suis donc intéressé aux *auto-encodeurs* implémentés par des réseaux de neurones profonds.

Introduction à l’apprentissage supervisé et aux auto-encodeurs

Pour les personnes non familières avec l’apprentissage supervisé, je vais d’abord l’introduire de manière simple en faisant référence à un problème d’optimisation.

A partir d’un jeu de données où chacune est étiquetée au travers de une ou plusieurs caractéristiques (des images d’animaux où sont précisées le poids du spécimen ou encore son espèce par exemple), un algorithme “f” doit apprendre automatiquement quelle est la caractéristique “y” associée à une donnée “x” dans un jeu de données “D”.

Pour y parvenir, l’algorithme optimise ses paramètres “θ” en évaluant son erreur vis-à-vis de la réalité, ce jugement étant la fonction de perte. Cette réalité est auparavant définie par un “oracle” qui détient la vérité, vous par exemple.

L’algorithme se règle pour minimiser son erreur si vous préférez.

\[\forall(x,y) \in D, \underset {\theta}{min} \left [ \frac {1}{|D|} \sum_{i=0}^{|D|}loss(y_i,f(x_i,\theta)) \right]\]

Par nature, les réseaux de neurones profonds sont tout à fait adaptés à l’apprentissage de représentations latentes : lorsqu’ils optimisent leur décision face à des données, ils apprennent par la même occasion une représentation interne (selon les réglages de l’utilisateur) censée faciliter la tâche de décision.

Prenons un exemple concret : la séparation du ou-exclusif (XOR) par une droite est impossible en deux dimensions. Elle le devient en passant en trois dimensions moyennant une projection entre les deux espaces. C’est cette projection que le réseau de neurones profond apprend en plus de sa décision (illustration ci-dessous).

Figure 1. Linear neural network — représentations latentes

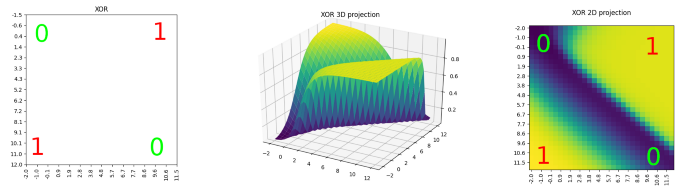
Passons maintenant à l’auto-encodeur.

Un auto-encodeur sert à encoder la donnée sous une forme différente de l’originale (un espace latent) pour ensuite la décoder et ainsi retrouver l’entrée initiale.

Figure 2. Auto-encodeur

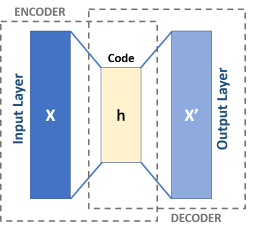
Il n’y a donc mathématiquement aucune différence avec les problèmes supervisés évoqués plus haut. Le seul changement étant que la caractéristique à prédire, la vérité ou le “y” si vous préférez, est la donnée elle-même.

Il ne nous reste maintenant qu’à mettre en pratique ces notions. Je vous propose d’utiliser la librairie Torch avec son wrapper PyTorch et comme vous l’avez deviné, Python pour développer !

Étape 1 : pré-traiter les données

Avant de s’atteler à la création de modèles, commencez d’abord par charger les fichiers audio et les pré-traiter pour que ceux-ci soient sous la représentation machine acceptée par les réseaux de neurones.

La librairie SciPy permet de charger facilement des fichiers audio au format WAV :

Lecture d’un fichier WAV

import numpy as np
from scipy.io import wavfile

from typing import Tuple

def open_wav(wav_path: str, nb_sec: int) -> Tuple[int, np.ndarray]:
    assert nb_sec > 0, f"Split length must be > 0 (actual == {nb_sec})."

    sampling_rate, data = wavfile.read(wav_path)

    split_size = sampling_rate * nb_sec
    nb_split = data.shape[0] // split_size

    splitted_audio = np.asarray(np.split(data[:split_size * nb_split], nb_split))

    int_size = splitted_audio.itemsize * 8.

    splitted_audio = splitted_audio.astype(np.float16)
    splitted_audio[:, :, 0] = splitted_audio[:, :, 0] / (2. ** int_size) * 2.
    splitted_audio[:, :, 1] = splitted_audio[:, :, 1] / (2. ** int_size) * 2.

    return sampling_rate, splitted_audio.mean(axis=2)

À ce stade le signal audio numérique est présent sous la forme d’une matrice (numpy.ndarray) contenant la moyenne des canaux droite et gauche découpée en segments de n secondes.

Je vous propose ensuite de passer dans le domaine fréquentiel grâce à la transformée de Fourier (ou FFT, ici discrète).

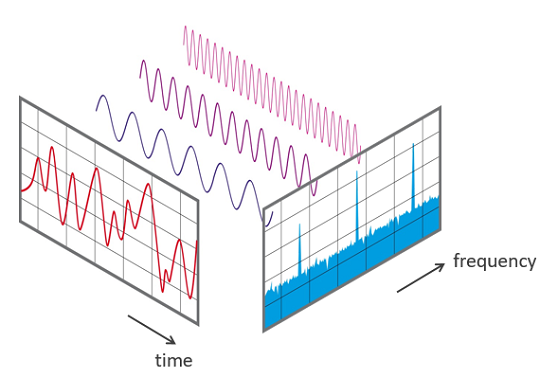
Transformée de Fourier

De cette façon le signal audio tel qu’observé sur un oscilloscope est converti dans le domaine fréquentiel. J’ai choisi de ne pas travailler sur le signal brut pour deux raisons : l’échelle de temps de la donnée est réduite à l’inverse de la quantité d’information par pas de temps qui se voit enrichie des fréquences de la FFT.

De plus, l’opération est je dirais “bijective” à l’inverse des spectrogrammes ce qui nous garantit de pouvoir retrouver un signal audio convenable si le modèle fonctionne.

La représentation par une transformée de Fourier discrète double la quantité d’octets de l’audio original (avec une représentation dans les complexes).

Calcul des fréquences avec FFT

import numpy as np
import scipy

def fft_raw_audio(raw_audio_split: np.ndarray, nfft: int) -> np.ndarray:
    assert len(raw_audio_split.shape) == 2, \
        f"Wrong audio shape len (actual == {len(raw_audio_split.shape)}, needed == 2)."

    assert raw_audio_split.dtype == np.float16, \
        f"Wrong ndarray dtype (actual == {raw_audio_split.dtype}, neede == {np.float16})."

    max_value = raw_audio_split.max()
    min_value = raw_audio_split.min()
    assert max_value <= 1.0 and min_value >= -1., \
        f"Raw audio values must be normlized between [-1., 1.] (actual == [{min_value}, {max_value}])."

    splitted_data = np.stack(np.hsplit(raw_audio_split, raw_audio_split.shape[-1] / nfft), axis=-2)
    return np.apply_along_axis(lambda sub_split: scipy.fft(sub_split), 2, splitted_data)

La transformée de Fourier rapide donne en sortie une liste de vecteurs de complexes, chaque vecteur ayant pour dimension la taille de fenêtre sur laquelle l’opération a été calculée.

Les parties réelle et imaginaire sont alors concaténées en un seul vecteur. Il ne reste plus qu’à appliquer ces opérations sur de multiples fichiers WAV pour constituer notre jeu de données.

Traitement d’un wav

import numpy as np
import torch as th

# ... import open_wav, fft_raw_audio

# a wav file
wav_file = "my_music.wav"

# FFT sample
n_fft = 49

# in seconds
split_duration = 1

# Open raw audio
sample_rate, raw_audio = open_wav(wav_file, split_duration)

# Convert to FFT
complex_fft_audio = fft_raw_audio(raw_audio, n_fft)

real_fft_audio = np.real(complex_fft_audio)
imag_fft_audio = np.imag(complex_fft_audio)

# Concatenate real & imag part
data_np = np.concatenate([real_fft_audio, imag_fft_audio], axis=2).transpose((0, 2, 1))

# Data ready for our models
data_th = th.tensor(data_np, dtype=th.float)
print(data_th.size())

Les fichiers audio sont maintenant prêts à être injectés dans le réseau de neurone, ce que je vais aborder dans l’étape suivante.

Étape 2 : créer l’auto-encodeur

Chaque pas de temps de la donnée temporelle est représenté par un vecteur de dimension FFT_window * 2. Pour encoder une succession de ces vecteurs dans un espace latent, une architecture à convolutions semble être le meilleur choix car elle peut réduire le facteur temporel tout en enrichissant les motifs de ses noyaux. Pour cette première expérimentation je vous propose d’utiliser des convolutions à une dimension, le choix d’analyser la sortie de la FFT telle une image n’étant pas à écarter (ie convolutions en 2D).

La dimension temporelle de l’audio est diminuée en ajoutant du pas aux fenêtres de convolution (paramètre “stride” dans PyTorch). L’opération inverse est effectuée avec des convolutions transposées pour la partie décodeur (Il existe de nombreuses vidéos sur le sujet des convolutions transposées, aussi j’invite les personnes qui souhaiteraient comprendre plus en détail le sujet à en visionner quelques-unes).

Figure 3. Pipeline de traitement

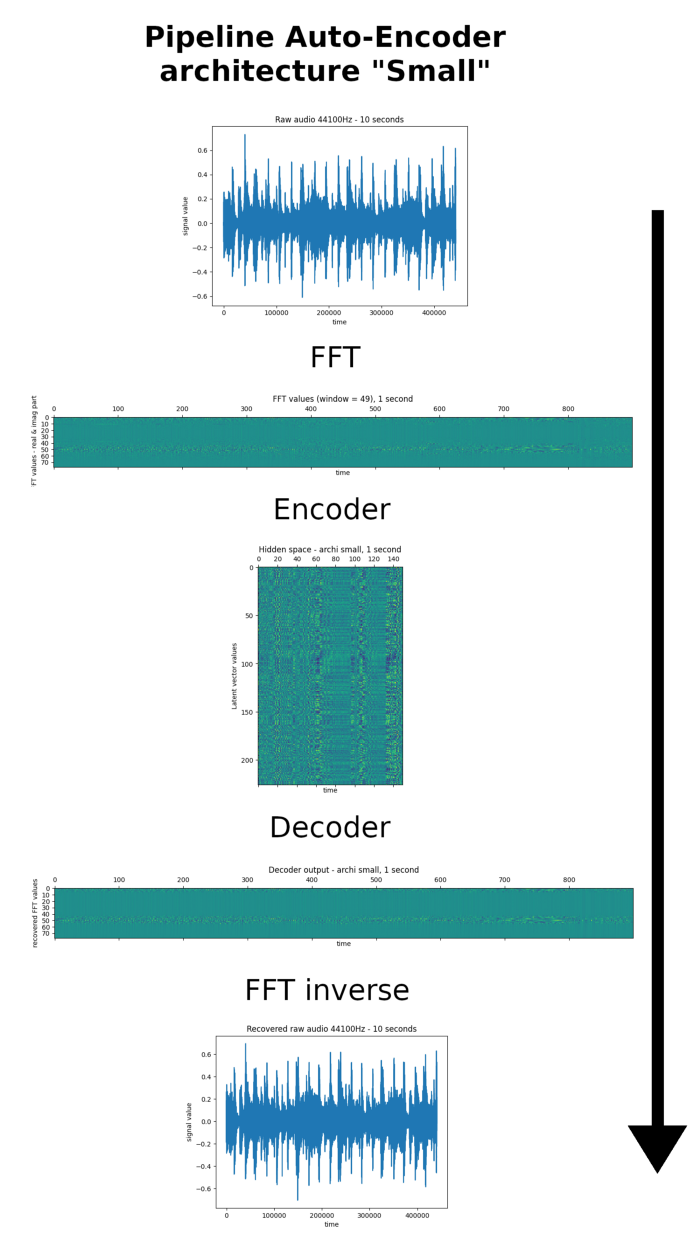
J’attire particulièrement votre attention sur la réduction temporelle pour la représentation latente. Attention, les signaux audio d’entrée et de sortie ne sont pas à la même échelle de temps que les matrices intermédiaires.

Ensuite, pour définir le taux de réduction temporel (“d” dans la formule plus bas) du réseau à convolutions, il faut impérativement que le nombre de pas de temps obtenu à la sortie de l’encodeur soit un entier, nous ne pouvons représenter un demi-vecteur. L’équation est la suivante sachant un échantillonnage de 44 100Hz et une longueur minimale de signal fixée à une seconde :

\[ f_s = 44100 \text{ Hz} , \Delta_t=1s\]

\[ \exists? \text{ }d \in \mathbb{N} \text{ et } N_{fft} \in \mathbb{N}, \frac{\frac{\Delta_t*f_s}{N_{fft}}}{d} \in \mathbb{N}\]

En cherchant le nombre de fréquences autorisant le plus de choix pour le facteur de divisons de notre transformée de Fourrier, 49 semble être le meilleur compromis entre richesse de la discrétisation des fréquences et diminution de l’échelle temporelle. Ainsi notre signal audio brut, une fois passé dans le domaine fréquentiel, sera représenté par 900 vecteurs de dimension 98 pour une seconde d’audio à 44 100Hz.

Les dimensions d’entrée de nos réseaux étant fixées, le premier modèle peut être implémenté. Ci-dessous le code pour l’encodeur et le décodeur “Small” :

Architecture Small

import torch as th
import torch.nn as nn


class EncoderSmall(nn.Module):
    def __init__(self, n_fft: int):
        super().__init__()

        n_channel = n_fft * 2

        self.cnn_enc = nn.Sequential(
            nn.Conv1d(n_channel, n_channel + 32,
                      kernel_size=3, padding=1),
            nn.BatchNorm1d(n_channel + 32),
            nn.Conv1d(n_channel + 32, n_channel + 64,
                      kernel_size=5, stride=2, padding=2),
            nn.BatchNorm1d(n_channel + 64),
            nn.Conv1d(n_channel + 64, n_channel + 128,
                      kernel_size=7, stride=3, padding=3),
            nn.BatchNorm1d(n_channel + 128)
        )

        self.n_channel = n_channel

    def forward(self, x):
        assert len(x.size()) == 3, \
            f"Wrong input size length, actual : {len(x.size())}, needed : {3}."
        assert x.size(1) == self.n_channel, \
            f"Wrong channel number, actual : {x.size(1)}, needed : {self.n_channel}."
        return self.cnn_enc(x)


class DecoderSmall(nn.Module):
    def __init__(self, n_fft: int):
        super().__init__()

        n_channel = n_fft * 2

        self.cnn_tr_dec = nn.Sequential(
            nn.ConvTranspose1d(n_channel + 128, n_channel + 64,
                               kernel_size=7, stride=3, padding=2),
            nn.BatchNorm1d(n_channel + 64),
            nn.ConvTranspose1d(n_channel + 64, n_channel + 32,
                               kernel_size=5, stride=2, output_padding=1, padding=2),
            nn.BatchNorm1d(n_channel + 32),
            nn.ConvTranspose1d(n_channel + 32, n_channel,
                               kernel_size=3, padding=1)
        )

        self.n_channel = n_channel + 128

    def forward(self, x):
        assert len(x.size()) == 3, \
            f"Wrong input size length, actual : {len(x.size())}, needed : {3}."
        assert x.size(1) == self.n_channel, \
            f"Wrong channel number, actual : {x.size(1)}, needed : {self.n_channel}."
        return self.cnn_tr_dec(x)

Maintenant que les données sont pré-traitées et le modèle créé, passez à l’étape d’apprentissage.

Étape 3 : entraîner l’auto-encodeur

Le code exécutant l’apprentissage diffère peu d’un code PyTorch classique : il y a toujours la propagation de la donnée à travers le réseau et le calcul de la fonction de perte (ici l’erreur moyenne au carré) sur laquelle on rétro-propage le gradient dans tout le réseau. L’étape finale consistant à mettre à jour les poids avec l’optimiseur (ici Adam — papier original).

AE main train script

import torch as th
import torch.nn as nn

# ...
# import EncoderSmall, DecoderSmall
# ...

# FFT window = 49
nfft = 49

# ...
# Use previous code to load musics
# ...

# data_th.size() must be equal to :
# (N_batch, nfft * 2, sample_rate / nfft)
data_th = th.tensor(..., dtype=np.float)

# Create Encoder and Decoder
enc = EncoderSmall(nfft)
dec = DecoderSmall(nfft)

# Create loss function
loss_fn = nn.MSELoss()

# Add Encoder and Decoder parameters to optimizer
optim = th.optim.Adam(list(enc.parameters()) + list(dec.parameters()), lr=1e-5)

# ...
# Loop over epoch and batch
# ...
  x_batch = # ... sample a batch

  # Encoder forward pass
  out_enc = enc(x_batch)

  # Decoder forward pass
  out_dec = dec(out_enc)

  # Compute MSE Loss
  loss = loss_fn(out_dec, x_batch)

  # Erase any previous gradient
  optim.zero_grad()

  # Backward on enc & dec
  loss.backward()

  # Update weights
  optim.step()

  # Print current loss value
  print("Current loss value : {:.6f}".format(loss.item()))

Voici une des forces de PyTorch à mes yeux : le calcul dynamique du graphe de calcul permet une certaine liberté dans l’organisation des opérations et modèles comme ici une séparation entre encodeur et décodeur. Ce qui s’avère extrêmement pratique.

Les différentes architectures essayées

J’ai mis en place et testé plusieurs architectures de CNN avec des scores variant selon leurs spécificités.

Figure 4. Résultats obtenus via les différentes architectures testées

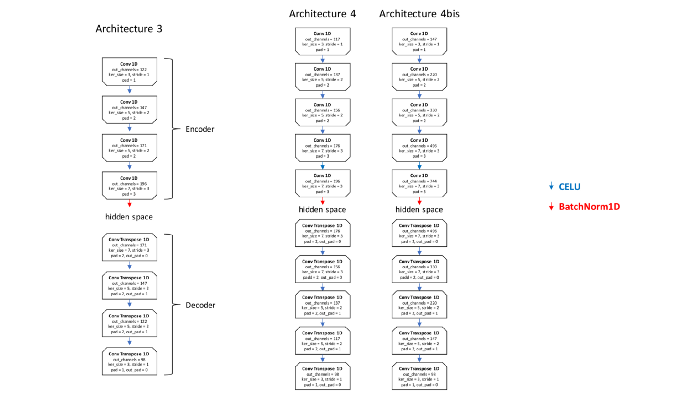
Trouver le bon compromis entre qualité de la sortie de décodeur et facteur de compression de la donnée constitue un des problèmes majeurs.

Les architectures 1 et 2 réduisent très nettement la dimension temporelle et n’augmentent pas proportionnellement la dimension d’un pas de temps. Les résultats sont médiocres ; que ce soit pour la fonction objectif ou pour la qualité sonore jugée par un humain.

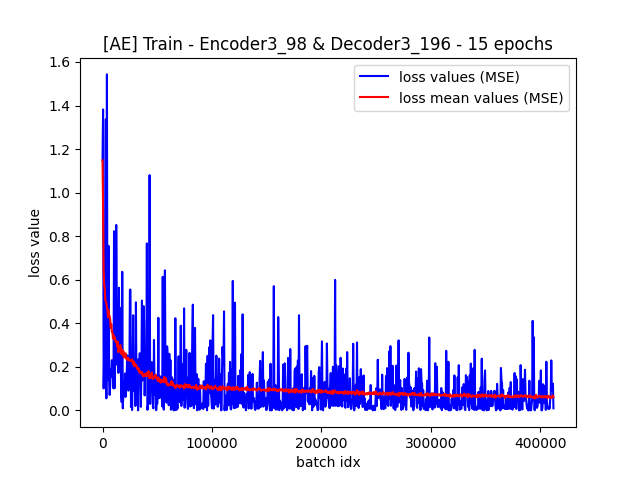
À l’inverse, la troisième architecture (resp. la “Small”) qui ne diminuait que de 12 (resp. 6) l’échelle temporelle tout en n’augmentant pas significativement la taille du vecteur de features, donne des résultats convenables (fonction objectif et écoute humaine) sur des audios non issus de l’ensemble d’apprentissage.

Il y a manifestement un dilemme entre compression pure (la quantité d’octets) et compression temporelle du signal audio.

Les architectures 3 et 4bis illustrent bien ce compromis. L’architecture 3 ne compresse pas beaucoup temporellement l’audio et n’augmente pas significativement la dimension des vecteurs. Les résultats sont corrects. Tandis que l’architecture 4bis, qui elle a un fort taux de compression temporel, augmente en conséquence la dimension de vecteurs en opposition à l’architecture 3 et permet ainsi des résultats plus corrects que sa version allégée (l’architecture 4).

Des modèle pré-entraînés sont disponible sur le GitHub du projet et permettent de produire une inférence sur un fichier audio WAV. Je vous laisse admirer le résultat !

L’enchaînement encodeur-décodeur fonctionne ce qui permet maintenant de tester l’idée qui a motivé mes travaux : générer un signal audio en utilisant uniquement la partie décodeur pré-entraînée dans laquelle on injecte une représentation latente aléatoire. Comme l’auto-encodeur a uniquement été entraîné à encoder un signal audio depuis des transformées de Fourier, les résultats de la génération aléatoire de musique depuis l’espace latent avec le décodeur pré-entraîné n’ont rien produit de satisfaisant.

En effet l’espace latent de l’auto-encodeur ne suit sûrement pas une distribution usuelle comme une distribution gaussienne. Ainsi, produire un espace latent aléatoire à partir d’une loi normale ne peut pas produire des résultats audio convenables. Je vous laisse tester le décodeur pré-entraîné et “admirer” l’atrocité musicale qui en résulte.

Je vous propose donc de tester une autre approche.

Étape 4 : réutiliser le décodeur avec un GAN

Les GAN (Generative Adversarial Networks, papier 2014) promettent des résultats rivalisant avec la donnée originale en terme de crédibilité. L’idée est la suivante : il faut entraîner un discriminateur à distinguer la vraie donnée de la fausse (celle issue de notre générateur) tout en optimisant le générateur pour produire une donnée semblable à la donnée réelle.

Dit autrement les deux modèles se “combattent” : le discriminateur essaie d’apprendre à reconnaître les fausses données issues du générateur alors que ce dernier apprend à tromper le discriminateur en générant des fausses données ressemblant aux vraies. Ainsi les fausses données issues du générateur doivent en théorie, lorsque le GAN a convergé, ressembler aux données réelles à partir desquelles il a été entraîné.

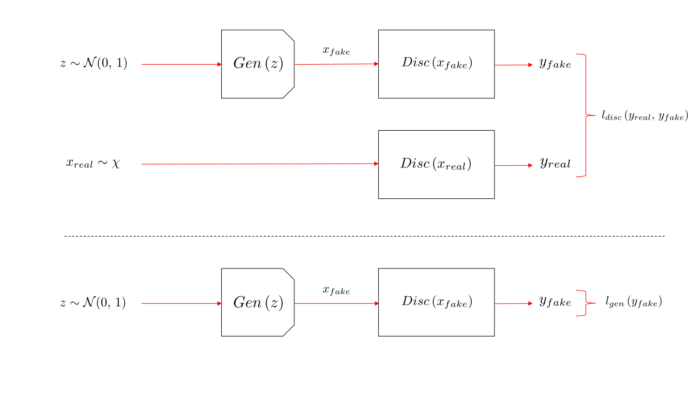
Voici les deux fonctions objectif qu’il faut optimiser, à savoir celle du discriminateur et celle du générateur :

\[l_{disc}= -(\log_2(Disc(x_{real}))+ \log_2(1-Disc(x_{fake})))\]

\[l_{gen}= -\log_2(Disc(x_{fake})))\]

Ces deux fonctions objectifs s’implémentent de la manière suivante :

import torch as th

def discriminator_loss(y_real: th.Tensor, y_fake: th.Tensor) -> th.Tensor:
    assert len(y_real.size()) == 1, \
        f"Wrong y_real size, actual : {y_real.size()}, needed : (N)."
    assert len(y_fake.size()) == 1, \
        f"Wrong y_fake size, actual : {y_fake.size()}, needed : (N)."
    assert y_real.size(0) == y_fake.size(0), \
        f"y_real and y_fake must have the same batch size, y_real : {y_real.size(0)} and y_fake : {y_fake.size(0)}"

    return -th.mean(th.log2(y_real) + th.log2(1. - y_fake), dim=0)


def generator_loss(y_fake: th.Tensor) -> th.Tensor:
    assert len(y_fake.size()) == 1, \
        f"Wrong y_fake size, actual : {y_fake.size()}, needed : (N)."

    return -th.mean(th.log2(y_fake), dim=0)

Lorsque le discriminateur est entraîné seul avec un décodeur non ou pré-entraîné, utiliser un réseau à convolution pour extraire des motifs suivis de couches linéaires à des fins de classification permet d’obtenir des résultats très satisfaisants.

import torch as th
import torch.nn as nn

class DiscriminatorCNN(nn.Module):
    def __init__(self, n_fft: int):
        super().__init__()

        self.n_channel = n_fft * 2

        self.cnn = nn.Sequential(
            nn.Conv1d(self.n_channel,
                      int(self.n_channel * 1.2),
                      kernel_size=3, padding=1),
            nn.CELU(),
            nn.Conv1d(int(self.n_channel * 1.2),
                      int(self.n_channel * 1.2 ** 2),
                      kernel_size=5, stride=2, padding=2),
            nn.CELU(),
            nn.Conv1d(int(self.n_channel * 1.2 ** 2),
                      int(self.n_channel * 1.2 ** 3),
                      kernel_size=5, stride=2, padding=2),
            nn.CELU(),
            nn.Conv1d(int(self.n_channel * 1.2 ** 3),
                      int(self.n_channel * 1.2 ** 4),
                      kernel_size=7, stride=3, padding=3),
            nn.CELU(),
            nn.Conv1d(int(self.n_channel * 1.2 ** 4),
                      int(self.n_channel * 1.2 ** 5),
                      kernel_size=7, stride=3, padding=3),
            nn.CELU()
        )

        self.classif = nn.Sequential(
            nn.Linear(int(self.n_channel * 1.2 ** 5) * 25, 6096),
            nn.CELU(),
            nn.Linear(6096, 1),
            nn.Sigmoid()
        )

    def forward(self, x):
        out = self.cnn(x)
        out = out.flatten(1, 2)
        out = self.classif(out)
        return out.view(-1)

Pour le générateur, je vous propose d’essayer de recycler un de nos décodeurs sans aucune hypothèse que cela fonctionne. Il ne faut pas écarter l’expérimentation d’autres architectures avec l’optique du générateur en tête.

Fonctions objectif, discriminateur et générateur prêts, il ne reste plus qu’à créer notre script d’apprentissage :

train script GAN

import torch as th
import torch.nn as nn

# ...
# import DecoderSmall, DiscriminatorCNN, loss_discriminator, loss_generator
# ...

# FFT window = 49
nfft = 49

# Sample rate = 44100Hz
sample_rate = 44100

# split seconds duration
nb_sec = 1

# ...
# Load musics
# ...

# data_th.size() == (N_batch, nfft * 2, sample_rate // nfft)
data_th = th.tensor(..., dtype=th.float)

gen = DecoderSmall(nfft)
disc = DiscriminatorCNN(nfft)

small_division_factor = 2 * 3

hidden_size = nb_sec * sample_rate // nfft // small_division_factor
hidden_channels = nfft * 2 + 128

optim_disc = th.optim.SGD(disc.parameters(), lr=1e-5)
optim_gen = th.optim.SGD(gen.parameters(), lr=1e-5)

# ...
# Loop over epochs and batchs
# ...
  x_real = # ... sample a batch

  # Train discriminator
  gen.eval()
  disc.train()

  z_fake = th.randn(x_real.size(0), hidden_channels, hidden_size,
                              dtype=th.float, device=th.device("cuda"))

  x_fake = gen(z_fake)

  out_real = disc(x_real)
  out_fake = disc(x_fake)

  loss_disc = discriminator_loss(out_real, out_fake)

  optim_disc.zero_grad()
  loss_disc.backward()
  optim_disc.step()

  # Train generator
  disc.eval()
  gen.train()

  z_fake = th.randn(x_real.size(0), hidden_channels, hidden_size,
                              dtype=th.float, device=th.device("cuda"))
  x_fake = gen(z_fake)
  out_fake = disc(x_fake)

  loss_gen = generator_loss(out_fake)

  optim_gen.zero_grad()
  loss_gen.backward()
  optim_gen.step()

  print(f"Loss disc = {loss_disc.item()}, loss gen = {loss_gen.item()}")

Voici la force de PyTorch avec la définition dynamique du graphe de calcul : il est possible de rétro-propager dans plusieurs modèles comme pour l’auto-encodeur, mais il est aussi possible de n’optimiser qu’un modèle en particulier pour une passe de rétro-propagation.

Un apprentissage difficile

L’entraînement du GAN s’est révélé très complexe. A ce jour je n’ai pas encore réussi à obtenir une réelle convergence des deux modèles.

Ce mode d’échec se matérialise de la manière suivante : le discriminateur converge lentement sur les premières époques, puis par la suite atteint son optimum faisant diverger très fortement le générateur empêchant d’atteindre le point d’équilibre. Ce point d’équilibre correspondant au discriminateur ne discernant plus les vrais des faux, soit un score de 2 pour le discriminateur et de 1 pour le générateur (log2).

Le discriminateur semble trop fort pour le générateur ce qui peut s’expliquer par les raisons suivantes :

le discriminateur a appris par cœur les données (c’est-à-dire du sur-apprentissage) et ne laisse pas le champ libre au générateur pour se perfectionner
le générateur (un des décodeurs que nous avons implémenté pour les auto-encodeurs) n’est peut être pas adapté à cette tâche et ne peut pas converger convenablement.

Figure 5. learning rates : disc = 2e-5, gen = 3e-4

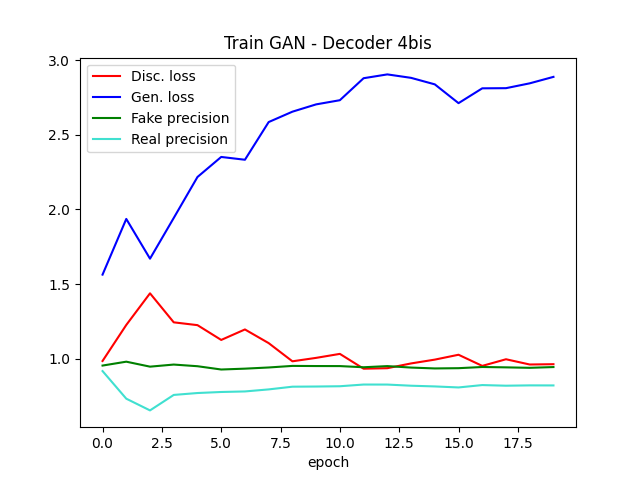
Il y a un réel compromis à trouver entre les “rapidités” de convergence des deux modèles.

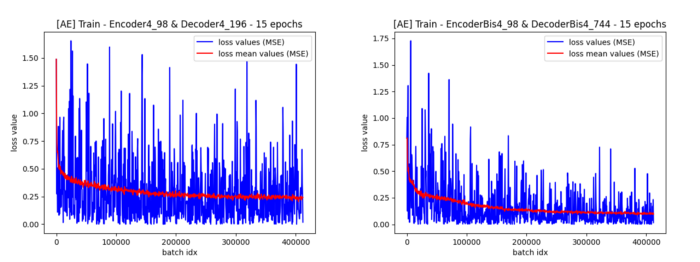
En simplifiant le modèle du discriminateur pour que celui soit en théorie plus faible et/ou en diminuant son taux d’apprentissage, il est possible de retarder le mode d’échec sur quelques époques comme le montrent les graphes ci-dessous :

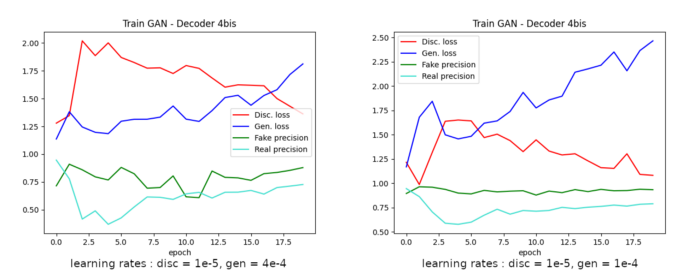
Le deuxième graphe permet d’observer que le générateur arrive à prendre le dessus sur le discriminateur entre les époques de 2 à 6. Notons que dans les deux cas où seul le taux d’apprentissage du générateur diffère (4e-4 pour le premier et 1e-4 pour le deuxième) le discriminateur finit par reprendre le dessus.

Les résultats le confirment car la qualité des audio générés laisse à désirer même pour une oreille peu expérimentée !

Les plus grands compositeurs ont encore un bel avenir devant eux

L’auto-encodeur n’est pas optimisé pour générer de l’audio aléatoirement et le GAN rentre en échec pour tout les tests effectués jusqu’à présent.

Figure 6. Image par MikesPhotos de Pixabay

Cependant, les modèles expérimentés (encodeurs, décodeurs / générateurs et discriminateurs)* fonctionnent bien de manière indépendante* : l’enchaînement encodeur puis décodeur montre des résultats prometteurs et le discriminateur peut converger seul de manière notoire. C’est lorsque le décodeur, utilisé en temps que générateur, marche de paire avec le discriminateur que l’optimisation multi-objectifs coince.

Dans les points d’exploration et d’approfondissement il serait intéressant d’explorer d’autres architectures notamment celles permettant d’analyser les vecteurs de FFT à la manière d’une image (convolution 2D). De plus l’échec de l’apprentissage du GAN n’a été mesuré que depuis les métriques de sortie et demanderait de ce fait un réel diagnostic.

Vous pouvez suivre l’avancement de la partie GAN sur mon projet GitHub qui est actuellement toujours en phase d’expérimentation.

Sources

lien GitHub : Ipsedo/MusicAutoEncoder
PyTorch homepage : https://pytorch.org/

Samuel Berrien

How to : un réseau neuronal artificiel peut-il rivaliser avec Bach ?