A la découverte d’un algorithme de machine learning peu conventionnel

Dans le cadre de mes recherches, j’ai été amené à étudier des solutions utilisant des systèmes multi-agents et du machine learning. J’ai notamment essayé de reproduire les résultats d’un article qui avait attiré mon attention : "Multi-Agent Image Classification via Reinforcement Learning".

L’algorithme qui y est décrit fait partie des plus singuliers qu’il m’ait été donné d’apprécier jusqu’ici. D’autant plus à des fins de classification d’images. En effet il fait appel à plusieurs approches : les systèmes multi-agents et, au sein du machine learning, à l’apprentissage supervisé et à l’apprentissage par renforcement.

Après avoir obtenu des premiers résultats qui ne furent pas aussi bon qu’escomptés, j’ai récemment décidé de reprendre mon projet GitHub. Je vous propose donc de décrire mon approche qui sera basée sur l’utilisation du framework PyTorch pour développer les réseaux de neurones (car il permet plus de laxité vis-à-vis du graphe de calcul du fait qu’il se détermine de manière dynamique), et vous l’avez deviné sur Python pour implémenter le tout.

Introduction aux systèmes multi-agents

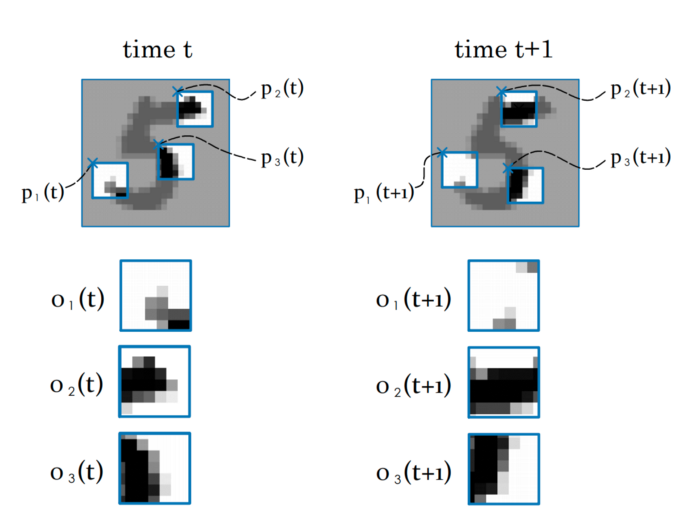
Le principe est le suivant : plusieurs agents observent à partir de différentes positions des sous parties d’images, telle qu’une vue de 10 par 10 pixels par exemple. A chaque itération, les agents doivent produire 3 résultats : une action pour l’itération suivante, une prédiction de la classe de l’image et un message destiné aux autres agents.

Dans notre cas, le modèle de l’algorithme reposera sur le même réseau de neurones pour tous les agents.

Figure 1. Illustration issue de l’article

La prédiction de la classe d’image se fait par vote moyen entre tout les agents. L'apprentissage supervisé permettant de réduire l’erreur vis-à-vis de la classe de l’image.

Les agents peuvent se déplacer au sein de l’image dans quatre directions. L’utilisation de la méthode d'apprentissage par renforcement permet à l’agent autonome d’optimiser le choix de l’action à effectuer. En effet, l’agent (notre algorithme) doit optimiser l’espérance de sa récompense, en d’autres termes il maximise la probabilité de gagner. Pour y parvenir il exploite son état dans l’environnement pour choisir l’action à effectuer.

Figure 2. Illustration issue de Wikimedia

Etape 1 : développer des réseaux de neurones

Je vous propose de débuter par le développement des réseaux de neurones avec le framework PyTorch !

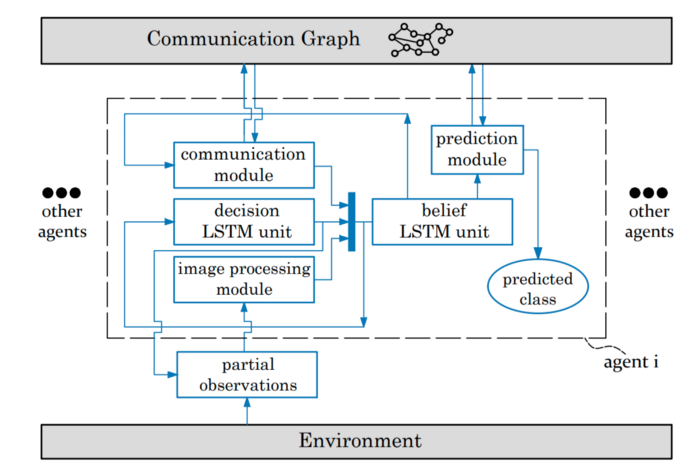
Graphe de calcul

Le modèle fait appel à 3 types de réseaux de neurones :

des réseaux linéaires (ou denses) utilisés pour les changements d’espace vectoriel ; constituant les modules de projection vers l’espace des messages, des actions et des classes,
des réseaux récurrents utilisés pour adresser la dimension temporelle de l’algorithme via les modules de décision et de croyance (belief),
des réseaux à convolutions utilisés pour le traitement de l’image permettant à l’algorithme d’extraire des caractéristiques depuis l’image, .

Le graphe de calcul peut paraître complexe, aussi je ne m’attarde pas sur sa description, cette dernière étant disponible dans l'article. Voici néanmoins un aperçu synthétique du graphe :

Figure 3. Graphe de calcul — issu de l’article

Extraire des caractéristiques

Pour implémenter le réseau à convolution, il est préférable de démarrer par une succession de deux couches. L’utilisation de davantage de couches pourrait augmenter l’espace de représentation des différents espaces latents du réseau ce qui lui complexifierait la tâche (malédiction des dimensions…).

Je vous propose donc de limiter la “difficulté” d’apprentissage du réseau en limitant l’espace de représentation. PyTorch fournit l’implémentation des convolutions à deux dimensions qui s’intègrent comme tout autre module :

Réseau à convolution

import torch.nn as nn

class MNISTCnn(nn.Module):
    """
    b_θ5 : R^f*f -> R^n
    """

    def __init__(self, f: int) -> None:
        super().__init__()

        self.__f = f

        self.seq_conv = nn.Sequential(
            nn.Conv2d(1, 3, kernel_size=3,
                      padding=1, padding_mode='zeros'),
            nn.ReLU(),
            nn.Conv2d(3, 6, kernel_size=3,
                      padding=1, padding_mode='zeros'),
            nn.ReLU()
        )

        self.__out_size = 6 * f ** 2

    def forward(self, o_t):
        o_t = o_t[:, 0, None, :, :]  # grey scale
        out = self.seq_conv(o_t)
        out = out.flatten(1, -1)
        return out

A noter ici que les dimensions d’entrée des noyaux sont configurées pour le MNIST, ce que j’aborde par la suite.

Projections linéaires

Le réseau de neurones comporte plusieurs sous modules effectuant des projections linéaires. Ces dernières projettent un vecteur d’entrée vers un espace latent comme celui des messages, ou vers un espace de sortie tel que celui des actions :

Réseau linéaire

import torch.nn as nn


class LinearModule(nn.Module):

    def __init__(self, in_dim: int, in_out: int,
                 hidden_size: int) -> None:
        super().__init__()

        self.seq_lin = nn.Sequential(
            nn.Linear(in_dim, hidden_size),
            nn.CELU(),
            nn.Linear(hidden_size, in_out)
        )

        for m in self.seq_lin:
            if isinstance(m, nn.Linear):
                nn.init.xavier_uniform_(m.weight)

    def forward(self, x):
        return self.seq_lin(x)

Il faudra prendre soin de respecter les rapports de tailles de dimension entre les différents réseaux linéaires (message, politique/action, prédiction). L’espace latent des messages doit être inférieur à celui des features (extraites avec le CNN) et supérieur à celui de l’état (la position sur le plan).

Belief & action

Pour intégrer le facteur temporel de l’algorithme, les auteurs de l’article s’orientent vers des réseaux récurrents type Long Short Term Memory (LSTM). Le premier des deux LSTM du réseau constitue le module de décision de l’algorithme. Quant au deuxième, il permet d’affiner la croyance du système multi-agents à une étape donnée.

Les deux réseaux LSTM utilisent en entrée le même vecteur : la concaténation de l’observation, du message moyen et de l’état. Les vecteurs cachés sont issus de l’ancienne itération pour le premier (decision unit) et de la sortie du premier pour le deuxième (belief unit). J’utilise le Module PyTorch LSTMCell car je déploie le réseau récurrent sur une seule étape à la fois :

Réseau récurrent — LSTM

import torch.nn as nn

class LSTMCellWrapper(nn.Module):
    # f_θ1 & f_θ2

    def __init__(self, input_size: int, n: int) -> None:
        super().__init__()

        self.lstm = nn.LSTMCell(input_size, n)

    def forward(self, h, c, u):
        nb_ag, batch_size, hidden_size = h.size()

        h, c, u = \
            h.flatten(0, 1), \
            c.flatten(0, 1), \
            u.flatten(0, 1)

        h_next, c_next = self.lstm(u, (h, c))

        return h_next.view(nb_ag, batch_size, -1), \
               c_next.view(nb_ag, batch_size, -1)

De nombreux articles et tutoriels vous expliqueront de manière parfaite le fonctionnement des LSTM sur lesquels je vous recommande de vous attarder!

Etape 2 : encapsuler les réseaux

Les différents réseaux étant prêts à l’emploi, il ne manque plus qu’à les encapsuler dans un Module PyTorch pour faciliter leurs manipulations (il est plus simple de n’avoir qu’un seul objet, que ce soit pour retrouver les paramètres à optimiser ou pour factoriser le code) ce que propose le module ModuleDict. Il s’agit d’un mappage clef vers Module très utile pour facilement retrouver les réseaux :

Wrapper des réseaux de neurones

import torch.nn as nn

class LinearModule(nn.Module):
  pass

class LSTMCellWrapper(nn.Module):
  pass

class MNISTCnn(nn.Module):
  pass

window_size = 6
nb_action = 4
cnn_out_size = 6 * window_size ** 2
nb_class = 10

n = 128
n_m = 32
n_l = 192

d = 2
n_d = 6

networks_dict = nn.ModuleDict({
    "map_obs": MNISTCnn(window_size),
    "map_pos": LinearModule(n, n_d, 8),
    "evaluate_msg": LinearModule(n, n_m, n_l),
    "belief_unit": LSTMCellWrapper(
        cnn_out_size + n_d + n_m, n),
    "action_unit": LSTMCellWrapper(
        cnn_out_size + n_d + n_m, n),
    "policy": LinearModule(nb_action, n, n_l),
    "predict": LinearModule(n, nb_class, n_l)
})

Observation et transition

Il vous reste maintenant à développer la partie essentielle de l’algorithme : les fonctions d’observation et de transition liées à l’apprentissage par renforcement de l’algorithme. Elles constitueront le cœur du modèle de transition de l’environnement.

L’observation doit, à partir d’une liste de position et d’une taille de vue des agents (10 par 10 pixels par exemple), retourner une liste de sous parties d’image. Pour la transition, il faut simplement mettre à jour une liste de positions selon une liste d’actions. Voici les deux fonctions en questions :

Fonctions de transition et d’observation

import torch as th


def trans_img(pos: th.Tensor, a_t_next: th.Tensor,
              f: int, img_size: int) -> th.Tensor:

    new_pos = pos.clone()

    idx = (new_pos[:, :, 0] + a_t_next[:, :, 0] >= 0) * \
          (new_pos[:, :, 0] + a_t_next[:, :, 0] + f < img_size) * \
          (new_pos[:, :, 1] + a_t_next[:, :, 1] >= 0) * \
          (new_pos[:, :, 1] + a_t_next[:, :, 1] + f < img_size)

    idx = idx.unsqueeze(2).to(th.float)

    return idx * (new_pos + a_t_next) + (1 - idx) * new_pos


def obs_img(img: th.Tensor, pos: th.Tensor, f: int) -> th.Tensor:

    nb_a, b_pos, d = pos.size()
    b_img, c, h, w = img.size()

    # pos.size == (nb_ag, batch_size, 2)
    pos_min = pos
    pos_max = pos_min + f

    values_x = th.arange(0, w, device=pos.device)
    mask_x = (pos_min[:, :, 0, None] <= values_x.view(1, 1, w)) & \
             (values_x.view(1, 1, w) < pos_max[:, :, 0, None])

    values_y = th.arange(0, h, device=pos.device)
    mask_y = (pos_min[:, :, 1, None] <= values_y.view(1, 1, h)) & \
             (values_y.view(1, 1, h) < pos_max[:, :, 1, None])

    mask = mask_x.unsqueeze(-2) & mask_y.unsqueeze(-1)

    return img.unsqueeze(0).masked_select(mask.unsqueeze(-3)) \
        .view(nb_a, b_img, c, f, f)

Le système multi-agents

Je vous propose ensuite de représenter le système multi-agents à travers l’environnement d’apprentissage par renforcement. Voici la signature de la nouvelle classe :

Signature de la classe MultiAgent

import torch as th
import torch.nn as nn
from typing import Callable, Tuple


class MultiAgent:
    def __init__(
            self, nb_agents: int, model_wrapper: nn.ModuleDict,
            n: int, f: int, n_m: int, nb_action: int,
            obs: Callable[[th.Tensor, th.Tensor, int], th.Tensor],
            trans: Callable[[th.Tensor, th.Tensor, int, int], th.Tensor]
    ) -> None:
        pass

    def new_episode(self, batch_size: int, img_size: int) -> None:
        pass

    def step(self, img: th.Tensor, eps: float) -> None:
        pass

    def predict(self) -> Tuple[th.Tensor, th.Tensor]:
        # retourne un tuple <probabilité par action, probabilité par classe>
        pass

Se pose alors la question du déroulé d’une étape pour notre système multi-agents.

A noter que j’ai opté pour que les agents soient intégrés au réseau de neurones en temps que batch au même titre que les images. Ce afin d’optimiser le temps exécution (cela évite d’itérer sur tout les agents et permet de bénéficier des accélérations notoires avec le calcul GPU).

Voici le “code” de l’algorithme, dont je détaille uniquement la boucle principale ie celle allant des étapes t = 0 à T :

Figure 4. Pseudo code — issu de l’article

Une étape se déroule comme suit :

extraire les observations pour chaque agent (les bouts d’image) et donner cette observation en entrée à notre CNN
décoder puis calculer la moyenne des messages de l’étape précédente et passer l’état de l’agent dans l’espace latent
construire le vecteur u et l’injecter dans les deux LSTM
être mis à jour via la politique des actions et prendre la plus probable
Générer une prédiction

Il ne reste alors plus qu’à appliquer la succession d’opérations suivantes en version Python comme ci-après :

Extrait de la méthode step de la classe MultiAgent

import torch as th
import torch.nn as nn

#############
# Fake init #
#############

window_size = 6
nb_action = 4
cnn_out_size = 6 * window_size ** 2
nb_class = 10

n = 128
n_m = 32
n_l = 192

nb_agent = 3
d = 2
window_size = 6

actions = th.tensor([[1., 0.], [-1., 0.], [0., 1.], [0., -1.]])

batch_size = 5

img = th.rand(batch_size, 1, 28, 28)
pos = th.randint(0, 28, (nb_agent, d))

size = img.size(-1)

last_msg = th.rand(nb_agent, n_m)

last_h = th.rand(nb_agent, batch_size, n)
last_c = th.rand(nb_agent, batch_size, n)

last_h_caret = th.rand(nb_agent, batch_size, n)
last_c_caret = th.rand(nb_agent, batch_size, n)

#############
# Step code #
#############

# Observation
o_t = obs_img(img, pos, window_size)

# Feature space
# CNN need (N, C, W, H) not (N1, ..., N18, C, W, H)
b_t = networks_dict["map_obs"](o_t.flatten(0, -4))\
    .view(nb_agent, batch_size, -1)

# Get messages
# d_bar_t_tmp = self.__networks(self.__networks.decode_msg,
#                              self.msg[self.__t])
d_bar_t_tmp = last_msg
# Mean on agent
d_bar_t_mean = d_bar_t_tmp.mean(dim=0)
d_bar_t = ((d_bar_t_mean * nb_agent) - d_bar_t_tmp) \
          / (nb_agent - 1)

# Map pos in feature space
norm_pos = pos.to(th.float) \
           / th.tensor([[[img.size(-2), img.size(-1)]]])
lambda_t = networks_dict["map_pos"](norm_pos)

# LSTMs input
u_t = th.cat((b_t, d_bar_t, lambda_t), dim=2)

# Belief LSTM
h_t_next, c_t_next = networks_dict[
    "belief_unit"](
    last_h,
    last_c,
    u_t
)

# Evaluate message
next_msg = networks_dict["evaluate_msg"](h_t_next)

# Action unit LSTM
h_caret_t_next, c_caret_t_next = networks_dict["action_unit"](
    last_h_caret,
    last_c_caret,
    u_t
)

# Get action probabilities
action_scores = networks_dict["policy"](
    h_caret_t_next
)

# Greedy policy
prob, policy_actions = action_scores.max(dim=-1)

a_t_next = actions[policy_actions.view(-1)] \
    .view(nb_agent,
          batch_size,
          actions.size(-1))

# Apply action / Upgrade agent state
new_pos = trans_img(
    pos.to(th.float),
    a_t_next, window_size,
    size
).to(th.long)

L’apprentissage

L’apprentissage est relativement classique hormis cette nuance : nous n’optimisons pas seulement la réduction de l’erreur mais aussi la probabilité de choisir une action (un déplacement par agent) amenant à cette erreur. Cela s’effectue en maximisant l’espérance de “moins l’erreur”, comme si l’erreur était une récompense si nous prenions le négatif de cette dernière. Ainsi tout les modules du réseau sont atteints par la rétro-propagation, (ce qui est un des principaux atouts de PyTorch à mes yeux) :

Extrait de la boucle principale d’apprentissage

import torch as th
import torch.nn as nn

class MultiAgent:
    pass

nb_class = 10

networks_dict = nn.ModuleDict(...)
marl = MultiAgent(...)
optim = th.optim.Adam(networks_dict.parameters(), lr=1e-4)

# fake image
x_train, y_train = th.rand(5, 1, 28, 28), th.randint(0, 10, (5,))

# preds = [N_retry, N_batch, N_class]
# probas = [N_retry, N_batch]
# see https://github.com/Ipsedo/MARLClassification/blob/master/environment/core.py
preds, probas = episode_retry(...)

# Class one hot encoding
y_eye = th.eye(
    nb_class
)[y_train.unsqueeze(0)]

# pass to class proba (softmax)
preds = th.nn.functional.softmax(preds, dim=-1)

# L2 Loss - Classification error / reward
# reward = -error(y_true, y_step_pred).mean(class_dim)
r = -th.pow(y_eye - preds, 2.).mean(dim=-1)

# Compute loss
losses = probas * r.detach() + r

# Losses mean on images batch and trials
# maximize(E[reward]) -> minimize(-E[reward])
loss = -losses.mean()

# Reset gradient
optim.zero_grad()

# Backward on compute graph
loss.backward()

# Update weights
optim.step()

J’ai décrit ci-dessus les points les plus importants. Pour plus de détails, je vous invite à consulter mon projet GitHub..

Etape 3 : obtenir les premiers résultats

Je vous propose de d’abord tester l’algorithme avec les données du MNIST, l’objectif étant de reproduire les résultats présentés dans l’article.

Une fois cette étape validée, il s’agira d’exécuter l’apprentissage sur les images satellites du NWPU-RESISC45. Pourquoi ce jeu de données en particulier ? Car nous pouvons facilement imaginer les cas d’usage faisant appel à de la reconnaissance d’images dans un format contraint.

Test n°1 : MNIST

Le choix de ce jeu d’images me semble des plus approprié pour calculer un premier résultat. Pour ceux qui ne sont pas familiers avec ce dernier, ce jeu de données regroupe 60 000 images de chiffres manuscrits en niveau de gris. Il est idéal pour tester l’algorithme car il bénéficie en plus d’une normalisation qui le rend plus “simple” (rotation, alignement et normalisation).

Les résultats à reproduire sont de l’ordre de 98% de précision (pour rappel, les auteurs ayant donné les résultats selon différentes combinaison d’hyper-paramètres). Voici la liste que nous allons choisir pour l’entrainement :

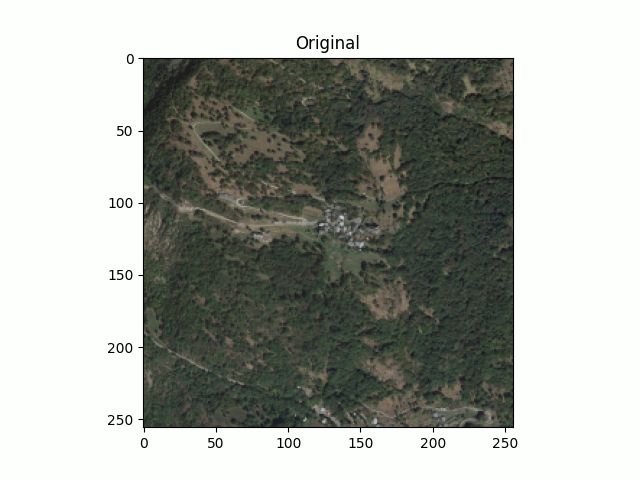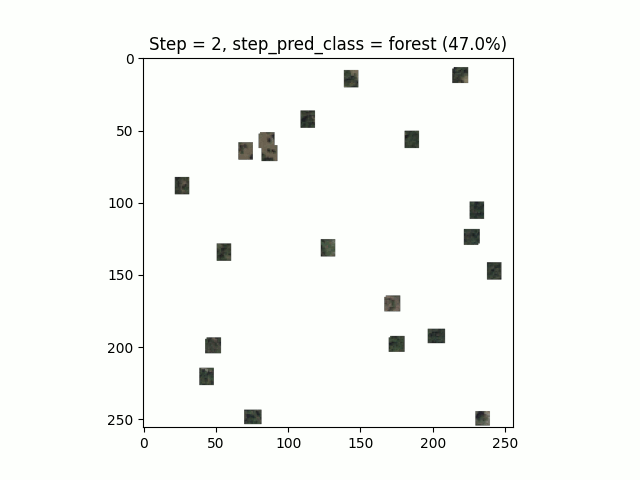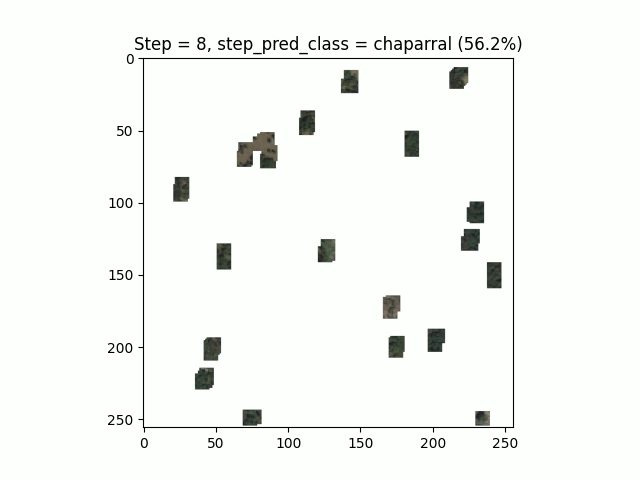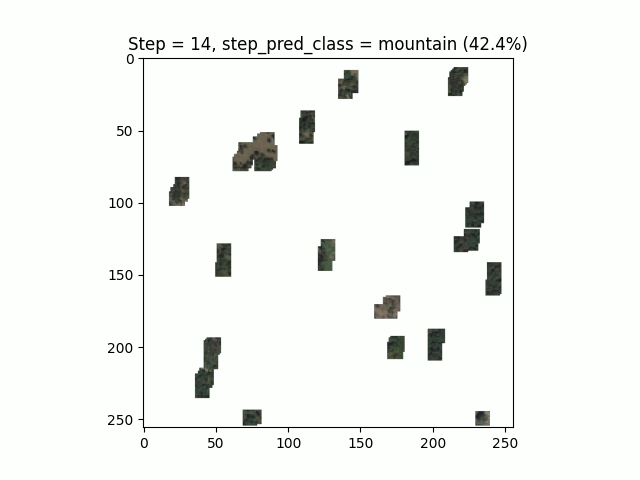
L’algorithme converge, c’est-à-dire qu’il semble reconnaître des chiffres manuscrits. L’optimum est atteint assez vite en une quinzaine d’époques avec une fenêtre de vue pour chaque agent de seulement 6 pixels !

Le résultat de l’inférence est plutôt agréable à visualiser, notre modèle sait reconnaître les zéros même en ne pouvant pas tout regarder :

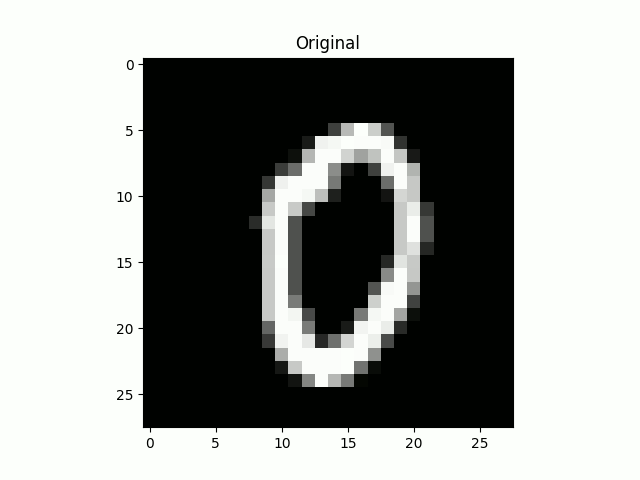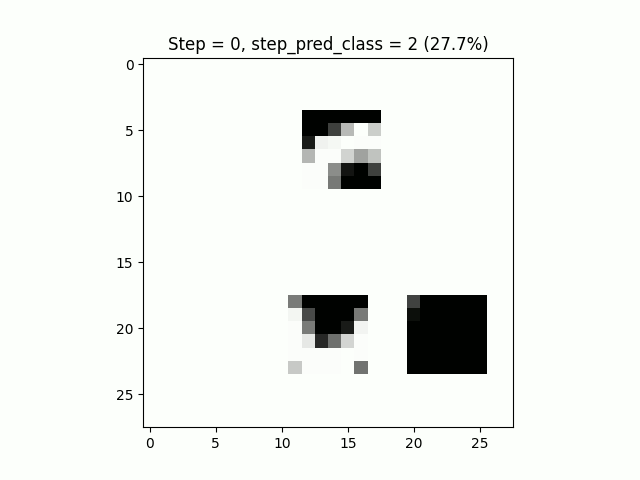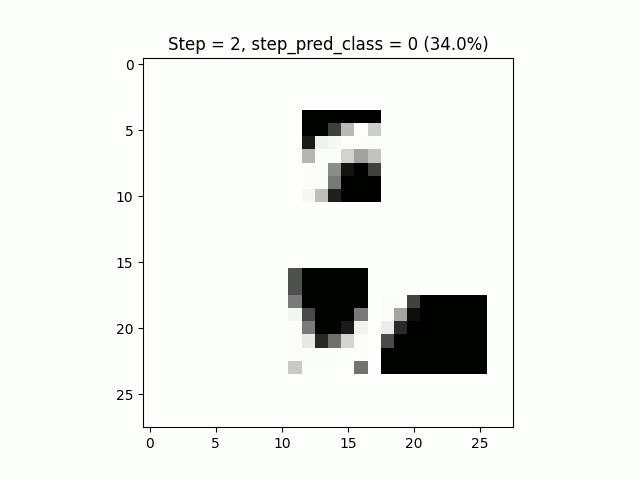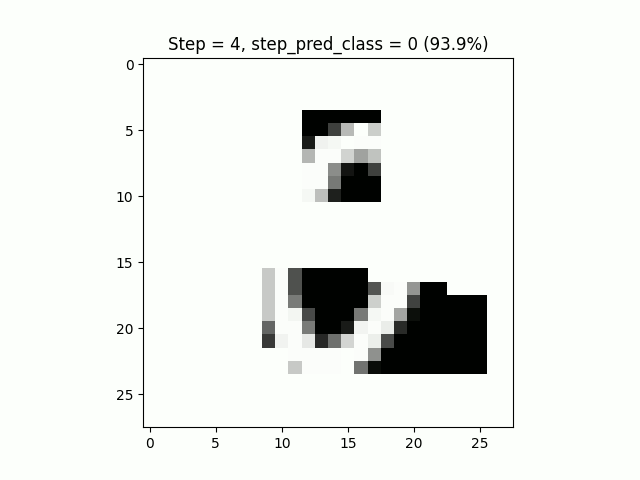
Il ne vous reste plus qu’à effectuer le même exercice sur un jeu de données un peu plus “complexe”.

Test n°2 : NWPU-RESISC45

Ce jeu d’images satellites regroupe 45 classes d’environnement terrestres à la fois naturel et urbains avec 700 images par classe. Une présentation plus approfondie des données est disponible au lien suivant : “Remote Sensing Image Scene Classification: Benchmark and State of the Art”.

Ses images étant en couleur, il vous faut d’abord légèrement modifier les canaux d’entrée du réseau à convolution pour 3 canaux (ie RGB).

Le choix des hyper-paramètres utilisés pour cet entrainement est contraint par la taille de sortie du réseau à convolution. Ceci dans le but de rester à la bonne échelle de grandeur et de limiter la malédiction des dimensions. Ci-dessous la liste des hyper-paramètres utilisés pour reproduire l’apprentissage sur NWPU-RESISC45 :

#agent	#steps	#class	image size	window size	hidden size	hidden size (message)	hidden size (state)	hidden size (output layer)	epsilon	#epoch	batch size	learning rate	#retry
45	15	45	256 * 256	10	1536	256	8	2048	2e-2	30	6	2.5e-5	1

#agent

#steps

#class

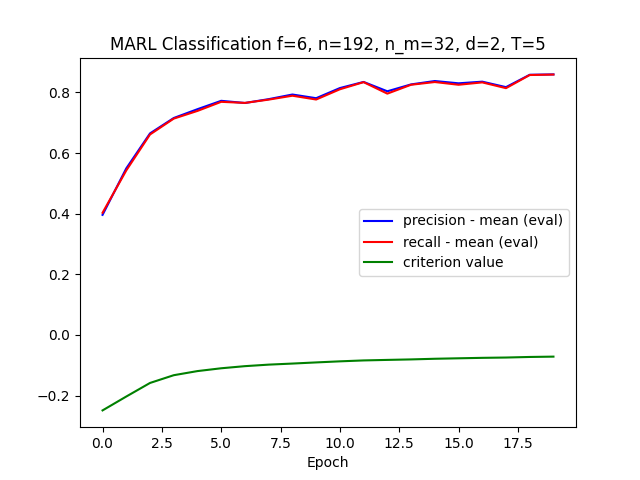
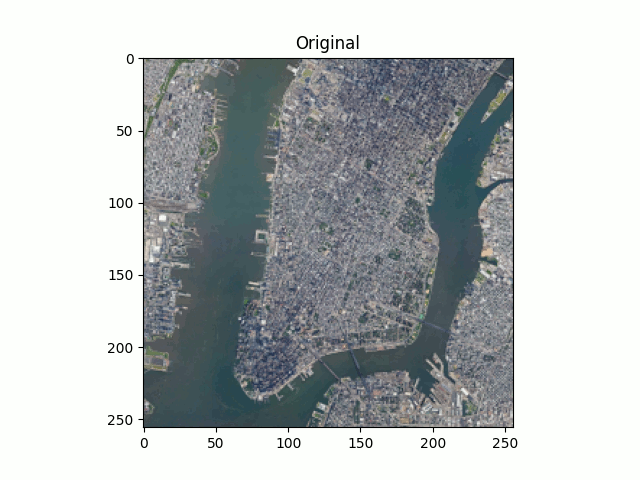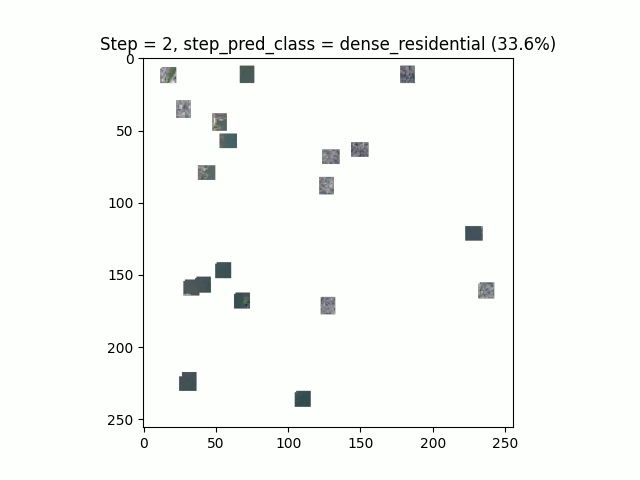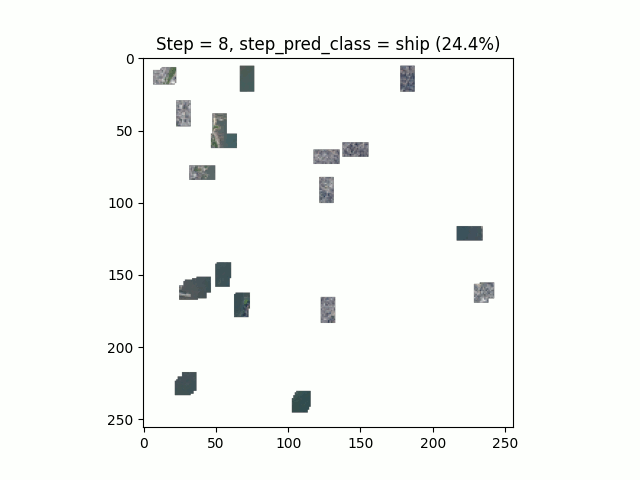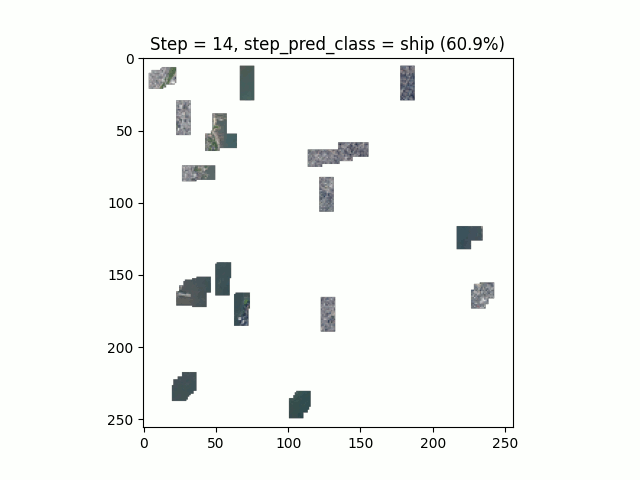
image size

window size

hidden size

hidden size (message)

hidden size (state)

hidden size (output layer)

epsilon

#epoch

batch size

learning rate

#retry

256 * 256

1536

256

2048

2e-2

2.5e-5

Les performances de l’algorithme sur ce jeu de données sont moindres que sur le MNIST. La limite de convergence avec ces hyper-paramètres est atteinte au bout d’une trentaine d’époques :

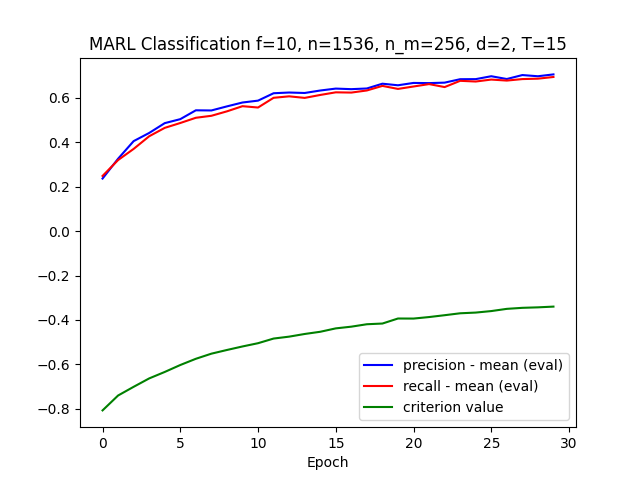
En s’intéressant de plus près aux résultats, nous pouvons observer un fort déséquilibre entre les classes. Certaines classes, comme les courts de tennis, ont un faible rappel (39%) et une précision correcte (68%) et inversement pour la classe “terrain de course”. Cela semble montrer que le modèle rentre en confusion sur certains environnements similaires.

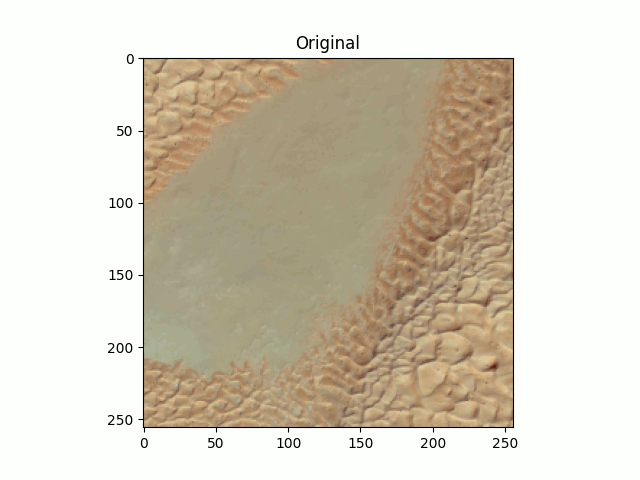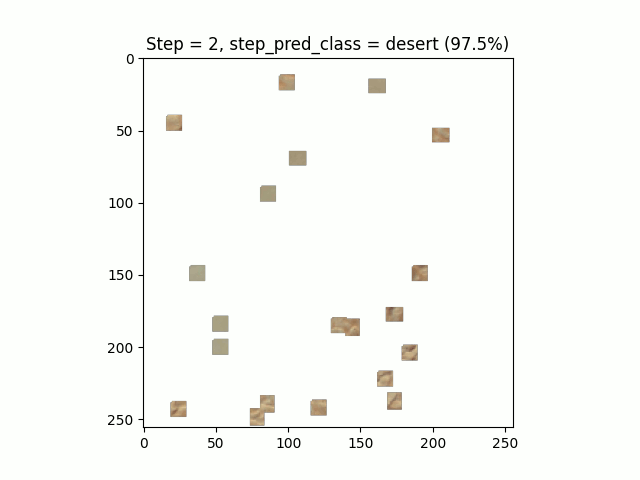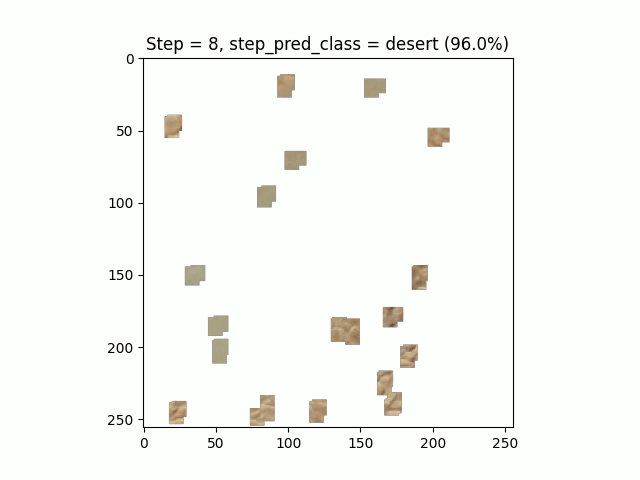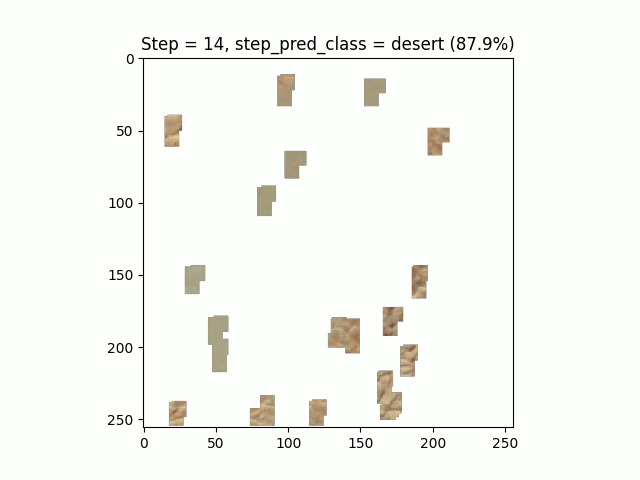
Pour expérimenter plus directement ce modèle, il est plus simple de trouver les images à inférer en se rendant sur Google Earth. Ci-dessous une capture de l’aéroport Charles De Gaulle :

Figure 5. Extrait depuis Google Earth

La technique décrite dans cet article est très intéressante car elle mêle plusieurs approches. Néanmoins, il semble qu’il faille nuancer la pertinence de chacune de ces dernières. En effet, je ne suis pas parvenu à démontrer ou réfuter l’utilité de l’apprentissage par renforcement (optimisation de l’espérance). Il faut plutôt mettre en avant le côté “boosting” de cet algorithme où chaque agent incarnerait un apprenant faible.

Néanmoins les résultats obtenus laissent entrevoir de nombreuses applications dans l’imagerie et plus particulièrement dans la classification d’images en milieu contraint, ce que font des drones par exemple. Dans ce contexte, la solution proposée par les auteurs a un double avantage :

la robustesse (l’algorithme est agnostique au nombre d’agents et ce même en pleine utilisation),
le coût puisque l’algorithme utilise, à chaque étape, seulement un trentième de l’image.