Alignements de k points

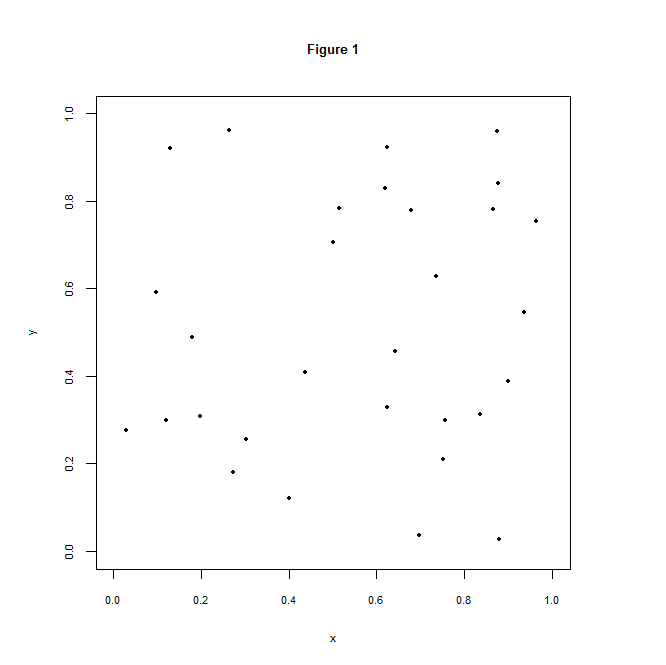
Dans le graphique ci-dessous, j’ai placé 30 points de façon (pseudo-)aléatoire — en l’occurrence, les coordonnées (\(x\) et \(y\)) suivent une loi uniforme continue entre 0 et 1. Question : à votre avis, combien d’alignements de 3 points peut-on trouver là-dedans ?

Celles et ceux qui me font l’honneur de me lire le devinent sans doute : il y en a beaucoup plus que ce que notre intuition nous suggère. C’est une forme d’illusion des séries (clustering illusion), ce biais cognitif qui nous porte à voir des phénomènes déterministes là où il n’y rien d’autre que de l’aléa. En l’espèce, nous aurons tendance à penser qu’un alignement de 3, 4 ou 5 points ne peut pas être dû au hasard : que quelqu’un l’a sans doute voulu comme ça.

Le problème

Commençons par poser les bases du problème : qu’est-ce qu’on entend par des points alignés, précisément. Par exemple, considérez le graphique suivant :

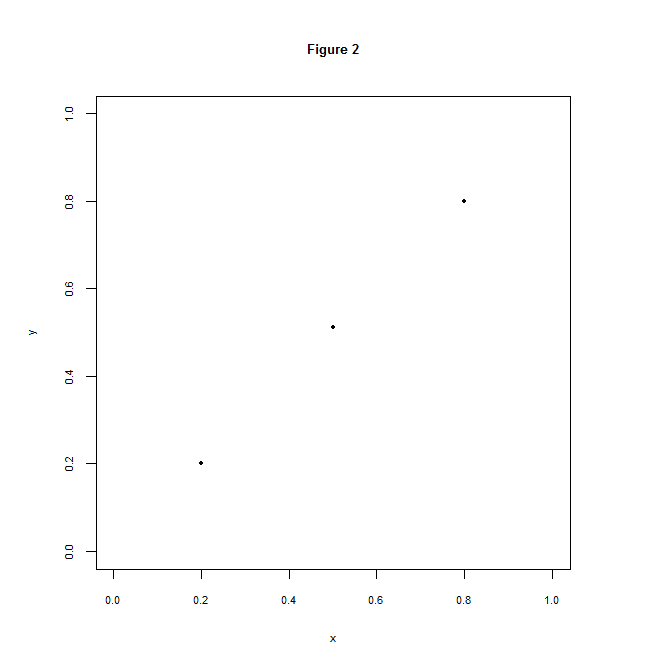
Au premier abord, ces trois points semblent bien alignés. Sauf qu’en traçant la droite de régression, ils sont raisonnablement alignés… mais pas parfaitement. :

Juger de l’alignement de \(k\) points, c’est donc une affaire de précision. Par points alignés, on entend habituellement qu’ils se trouvent tous dans une bande, un chemin rectiligne d’une largeur donnée. Sur le graphique ci-dessus, vous pouvez facilement imaginer deux droites parallèles à ma droite de régression — une un peu au-dessus, l’autre légèrement en dessous — de telle sorte que les trois points se trouvent dans cette zone du plan. Si cette bande a une largeur \(w\) et si vous estimez que ce degré de précision est suffisant, vous considérerez que ces points sont alignés.

Partant de là, on peut tenter d’estimer grossièrement la probabilité de trouver \(k\) points alignés dans un ensemble de \(n\) points situés dans un carré de côtés \(L\) avec une largeur de bande \(w\). Elle dépend du nombre de paquets de \(k\) points qu’il est possible de former parmi les \(n\) points (ce qui, dans un ensemble de 30 points \(n=30\) donne tout de même 4'060 triplets (i.e. \(k=3\)) possibles !) :

\[\binom{n}{k} = \frac{n!}{(n-k)!k!}\]

Et elle dépend du rapport entre la surface occupée par la bande (\(L \times w\)) et la surface totale du carré (\(L^2\)). Si vous considérez toutes les bandes contenant 2 points, le nombre de troisièmes points situés dans l’une de ces bandes devrait très approximativement être :

\[\frac{n!}{(n-k)!k!} \left(\frac{w}{L}\right)^{k-2}\]

Dans mon exemple, avec \(n=30\), \(k=3\), \(L=1\) et \(w=0.01\), ça devrait nous faire une quarantaine d’alignements de 3 points.

Simulation

Évidemment, j’ai eu envie de simuler ça sous R pour vérifier. Pour ce faire, j’ai concocté un petit algorithme que je soumets à votre sagacité. L’idée consiste, pour chaque \(k\)-uplet possible, à déterminer les coefficients de la droite de régression — la pente (\(\beta\)) et l’ordonnée à l’origine (\(\alpha\)) — puis, à vérifier que les \(k\) points se situent bien dans une bande de plus ou moins \(\frac{w}{2}\) autour de cette droite.

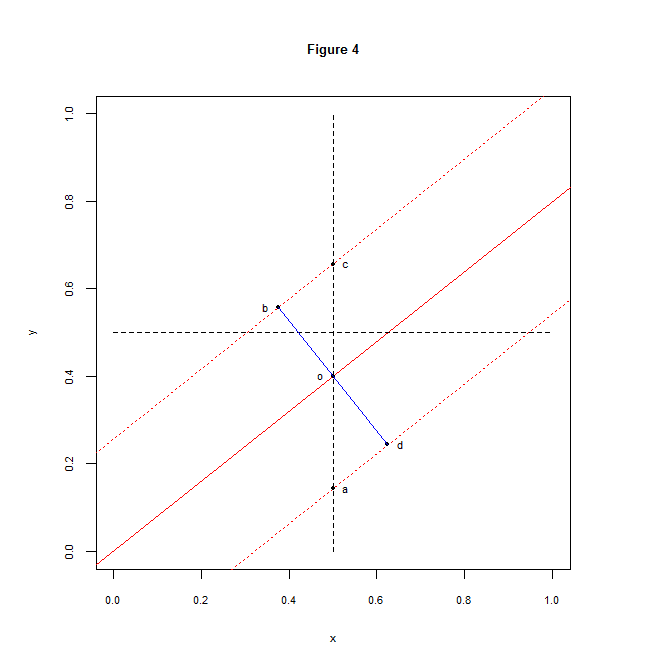
Dans le graphique ci-dessus, par exemple, nous souhaitons savoir si les \(k\) points sont situés à l’intérieur de la bande délimitée par les deux droites en pointillés rouges. Pour ce faire, il nous faut transformer les résidus de la régression (\(\varepsilon\)) en distances perpendiculaires à la droite de régression et vérifier que la longueur obtenue est bien inférieure à celle des segments [ob] ou [od] (en bleu), soit \(\frac{w}{2}\).

En principe, la valeur de l’angle [cob] (appelons-le \(\theta\)), en radians, doit être égale à l’arctangente de la pente de notre droite de régression (\(\beta\)) :

\[\theta = \arctan{\beta}\]

Et, par ailleurs :

\[\cos(\theta) = \frac{[ob]}{[oc]} = \frac{\frac{w}{2}}{\epsilon}\]

Avec un peu d’algèbre, nous cherchons donc à vérifier si :

\[\frac{\epsilon}{\cos(\theta)} \leq \frac{w}{2}\]

En faisant tourner cet algorithme sur tous les triplets possibles de mon set de \(n\) points ^[1] avec \(w = 0.01\), on vérifie qu’il y a pas moins de 47 alignements de 3 points :

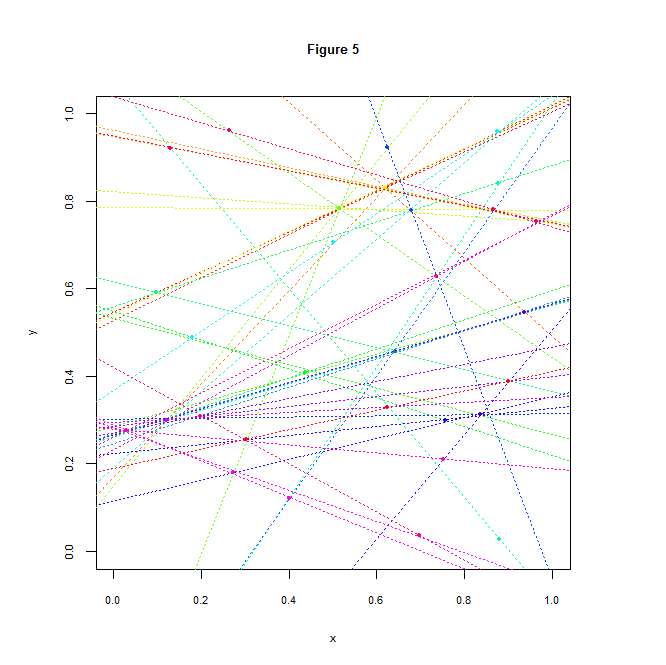
Et, si vous vous posiez la question, il y a aussi 4 alignements de 4 points :

Le code

Voici mon code sous R. Gardez en tête qu’il n’est clairement pas optimisé pour la vitesse d’exécution (et ce, d’autant plus que R est relativement lent ^[2]) : je vous recommande de vous contenter de petites valeurs pour n.

alignments = function(x, y, k = 3, w = 1/1000) {
	N <- length(x)
	I <- gtools:::combinations(N, k, 1:N)
	res <- list()
	j <- 0
	for(i in 1:nrow(I)) {
		xi <- x[I[i, ]]
		yi <- y[I[i, ]]
		ri <- lm(yi~1+xi)
		hh <- ri$res / cos(atan(ri$co[2]))
		if(all(hh <= w/2)) {
			tmp <- list(coef = unname(ri$co), x = xi, y = yi)
			j <- j + 1
			res[[j]] <- tmp
		}
	}
	return(res)
}

n <- 30
x <- runif(n)
y <- runif(n)
k <- 3
w <- 1/100
res <- alignments(x, y, k, w)
length(res)

cols <- rainbow(length(res))
op <- par(mar = rep(5, 4))
plot(x, y, cex.lab = .7, cex.axis = .7, pch = 16, cex = 1/2,
	xlim = 0:1, ylim = 0:1, main = "Figure 5", cex.main = .8)
for(i in 1:length(res)) {
	ri <- res[[i]]
	abline(ri$co[1], ri$co[2], lty = "dotted", col = cols[i])
	points(ri$x, ri$y, cex = 1/2, pch = 16, col = cols[i])
}
par(op)

1. Ce qui, j’en conviens volontiers, n’est sans doute pas la façon la plus rapide de faire.

2. Ceci étant dit, si quelqu’un trouve le courage de développer un algorithme plus efficient, je le publierai volontiers ici.

Guillaume Nicoulaud

Alignements de k points

Le problème

Simulation

Le code