Modéliser l’évolution des patrimoines avec une marche aléatoire

Au milieu du XIXe siècle, Jules Regnault (1834-1894) était courtier à la Bourse de Paris et désespérait comme beaucoup d’autre d’arriver à prévoir les mouvements du titre star de l’époque : la fameuse rente française 3% ^[1]. Constatant qu’il était incapable de deviner si le cours de cette obligation monterait ou baisserait le lendemain — et encore moins à horizon d’un an — il a eu une idée absolument géniale : faire « comme si » les cours de bourses étaient des processus stochastiques ^[2]. C’est la naissance de ce qui reste, encore aujourd’hui, un des piliers du calcul probabiliste sur les marchés financiers : la marche aléatoire.

En général et dans le domaine financier, les marches aléatoires sont utilisées pour modéliser les trajectoires possibles des rendements d’un actif (action, obligation, devise…) dans le temps. Il se trouve que c’est aussi un outil idéal pour conceptualiser l’évolution des patrimoines d’une population et, modulo quelques hypothèses, en tirer quelques conclusions que votre serviteur trouve particulièrement intéressantes.

Quelques précautions oratoires s’imposent : d’abord, nous allons raisonner en patrimoine brut (la valeur de tout ce que vous possédez) plutôt qu’en patrimoine net (la même chose, moins vos dettes) ; ce qui est très largement contestable ^[3]. Ensuite et surtout, ce qui suit est une version extrêmement simplifiée de ce qui pourrait être un bon modèle : cet article se borne a introduire quelques notions de base ; nous laisserons à d’autres le soin de l’adapter à des hypothèses plus réalistes.

Les maths

Considérez \(N\) patrimoines (avec \(i \in \{1, 2, \ldots, N\}\)) observés pendant \(T\) années (avec \(t \in \{1, 2, \ldots, T\}\)). Avec des rendements continus ^[4], la variation annuelle du patrimoine \(P_i\) de l’année \(t-1\) à l’année \(t\) s’écrit }:

\[\delta_{i, t} = \log{\left(P_{i, t}/P_{i, t-1}\right)} = \log{(P_{i, t})} - \log{(P_{i, t-1}})\]

Et la variation totale du patrimoine \(P_i\) au bout de \(T\) années est simplement la somme de ses variations annuelles }:

\[\delta_{i, T} = \sum_{t = 1}^T \delta_{i, t}\]

La valeur finale, à l’issue de ces \(T\) années, du patrimoine \(P_i\) s’écrit donc simplement :

\[P_{i, T} = P_{i, 0} \times e^{\delta_{i, T}}\]

Supposons que les variations annuelles de nos patrimoines suivent une distribution stable — peu importe laquelle ^[5] — de moyenne \(\mu\) et d’écart-type \(\sigma\). Au bout de \(T\) années, on sait que la variation moyenne (\(\mu_T\)) des patrimoines sera de donnée par :

\[\mu_T = \mu \times T\]

Si on admet que ces variations ne sont pas autocorrélées ^[6], la formule de Bienaymé nous permet d’écrire que l’écart-type au bout de \(T\) années (\(\sigma_T\)) sera de ^[7] ):

\[\sigma_T = \sigma \times \sqrt{T}\]

Par ailleurs, avec un nombre suffisant d’observations (ici d’années), le Théorème Central Limite nous apprend que la distribution des variations de nos \(N\) patrimoines sur \(T\) années suivra une loi normale — ou, du moins, quelque chose de proche — ce qui implique que la distribution des patrimoines eux-mêmes suivra une loi log-normale.

\[P_{i, T} \sim \mathcal{lnN}(\mu_T, \sigma_T^2)\]

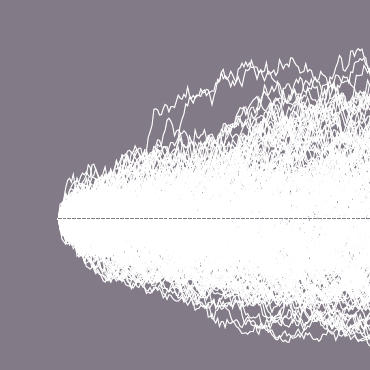
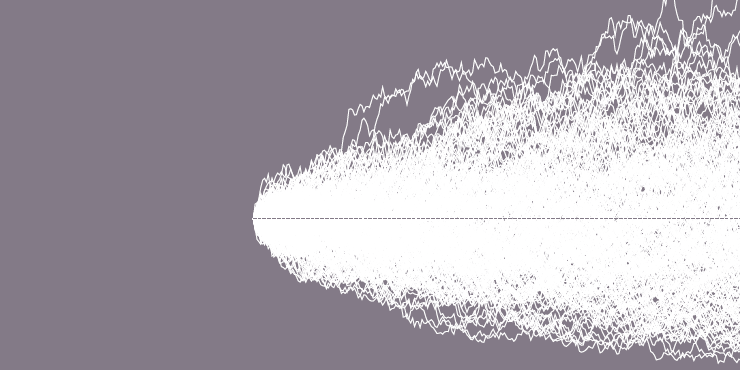
Forts de ce qui précède, on peut estimer précisément tous les quantiles de la distribution des patrimoines, sa déformation dans le temps et on peut surtout étudier comment la moyenne (\(\mu\)) et l’écart-type (\(\sigma\)) influent sur les inégalités patrimoniales. Graphiquement, la variation cumulée de nos \(N\) patrimoines dans le temps devrait ressembler à quelque chose comme ça :

Discussion

Je laisse les amateurs de simulations informatiques vérifier par eux-mêmes mais le résultat est sans appel }: plus la moyenne et l’écart-type sont élevés, plus les quantiles de patrimoine élevé (le seuil à partir duquel on appartient au fameux top 1%, par exemple) progressent plus vite que les autres (la médiane par exemple) — i.e. plus la distribution devient asymétrique à droite.

En d’autres termes, dans un monde (théorique) où les patrimoines évoluent de façon parfaitement aléatoire, un accroissement important des inégalités correspond à une situation dans laquelle (i) les gens, en moyenne, s’enrichissent beaucoup et/ou (ii) la variance des patrimoines est élevée. C’est exactement ce à quoi nous pouvons légitimement nous attendre dans un monde d’entrepreneurs : un patrimoine moyen qui progresse à un rythme élevé mais, en contrepartie, qui peut aussi baisser ou augmenter très vite (i.e. typiquement parce qu’il est principalement composé d’actions).

Au contraire, une situation dans laquelle les inégalités sont stables ou régressent correspond à un monde de patrimoines stationnaires (voire en régression) avec une faible variance. Nous sommes alors dans un monde de faible croissance dans lequel les riches sont des rentiers qui resteront riches générations après génération tandis que les pauvres n’ont aucun espoir de voir leur sort s’améliorer.

Il va de soi, je le disais en introduction, que ce modèle est extrêmement rustique et qu’il ne saurait servir à autre chose qu’illustrer ce dont nous venons de discuter. Dans la très longue liste des améliorations à y apporter, on peut lister :

Intégrer les inégalités de la distribution de départ (quand \(t=0\)), laquelle est évidemment asymétrique à droite (mais aussi traiter le phénomène de la division du capital entre héritiers ^[8]) ;
Tenir compte du fait que nous épargnons, mais pas tous au même rythme (ce qui est évidemment dû au niveau de nos revenus ^[9] mais aussi à des comportements individuels spécifiques) ;
Tenir compte du fait que nous n’investissons pas tous notre épargne sur les mêmes d’actifs : 62% du patrimoine des Français, par exemple, est constitué d’immobilier ; classe d’actifs bien moins volatile que les actions mais aussi bien moins rentable à long terme ^[10].

Toujours est-il que le constat auquel nous amène le modèle théorique exposé ci-dessus reste, me semble-t’il, valide : les inégalités patrimoniales que nous observons aujourd’hui sont une conséquence logique d’un monde dans lequel l’individu moyen s’enrichi et dans lequel les fortunes, notamment celles des plus fortunés, sont très volatiles.

1. C’était une obligation d’État perpétuelle (c’est-à-dire qu’elle versait 3% d’intérêt par an mais qu’il n’y avait aucune date de remboursement du capital prévue). Elle a été émise pour la première fois en 1825 et il faudra attendre 1982 pour que cet instrument de financement de l’État disparaisse définitivement.

2. On attribue souvent l’invention du concept de marche aléatoire au biostatisticien britannique Karl Pearson en 1905. C’est une erreur : c’est bien Regnault, dans Calcul des Chances et Philosophie de la Bourse (1863), qui en a été le découvreur.

3. Avec le patrimoine brut, notait l’économiste Alexandre Delaigue « un étudiant américain à Harvard, qui a pris un crédit pour faire ses études, est plus pauvre qu’un réfugié syrien qui cherche à survivre dans les montagnes libanaises. »

4. Vous devez raisonner en rendements continus parce que nous allons être amenés à les sommer — sauf, naturellement, si vous raisonnez directement en unités monétaires auquel cas vous pouvez même travailler sur des patrimoines nets (avec, potentiellement, des nombres négatifs).

5. Nous ne posons, contrairement à ce que semble penser un bon nombre de commentateurs, aucune hypothèse de normalité des rendements. Peu importe la distribution de base : notre seule hypothèse est sa stabilité ; notamment celle de sa moyenne et de son écart-type (ce qui, naturellement, est assez contestable).

6. Ce qui nous fait une deuxième hypothèse.

7. Les financiers parmi nous aurons reconnu la formule de la volatilité lorsque \(T\) périodes font un an : c’est, si vous l’ignoriez, exactement de là qu’elle vient.

8. Aujourd’hui, en France et en moyenne, on hérite après avoir fêté ses 50 printemps — c’est-à-dire à un âge où, objectivement, ce sont plutôt nos enfants qui auraient bien besoin d’un coup de pouce financier.

9. En théorie, le niveau de « richesse » d’un individu devrait être mesuré par la somme de son patrimoine net et de ses revenus futurs actualisés — en pratique, c’est évidemment un exercice extrêmement compliqué.

10. Je ne rentrerai pas ici dans le débat de la retraite par capitalisation et nous parlerons peut-être une autre fois de la valorisation de nos droits à la retraite par répartition (parce qu’évidemment, une rente à vie garantie par l’État, ça a une valeur considérable).

Guillaume Nicoulaud

Modéliser l’évolution des patrimoines avec une marche aléatoire

Les maths

Discussion